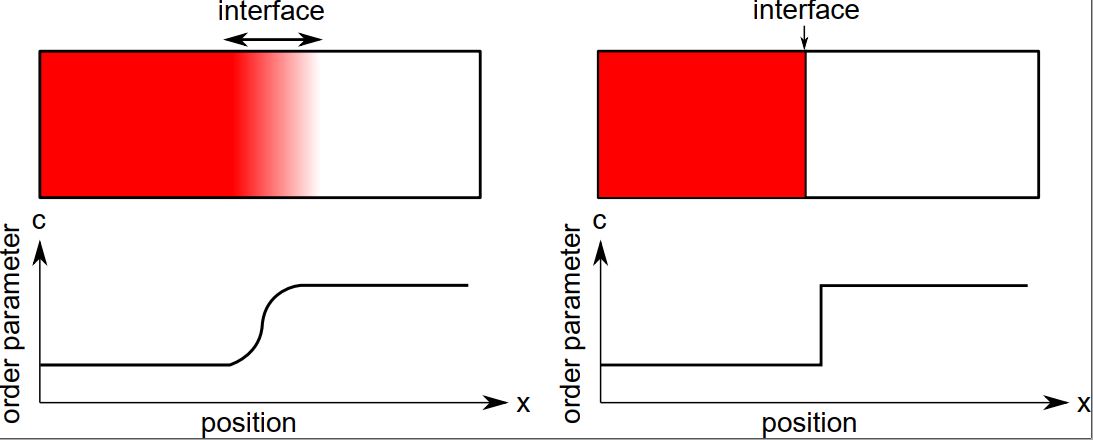
第一节课主要是叙述了“相”的概念以及两种不同的相边界模型(diffusive interface vs sharp interface)。第二节课的主题是相变(phase transition)。
相变是一个非平衡过程,描述起来比平衡过程要复杂。我们从最简单的Ising模型入手,对相变进行刻画。虽然数学模型较为简单,但是好处是可以定性地分析系统的特征温度、相变时对应的宏观物理量的变化。是研究复杂相变过程的基础。
Ising 模型最主要的假设有两个:
- 状态只有两种 +1 -1 (更为复杂的情况,状态可以描述为矢量等连续变化的量、甚至可以描述为波函数)
- 假设粒子只与最近的粒子发生相互作用(即只存在近场相互作用,无长程作用)
基于这两点出发,可以给出自旋粒子的哈密顿量。从哈密顿量出发、结合Gibbs概率密度分布(概率依能量指数分配),可推倒出粒子自旋量的概率测度(tanh分布,slide-12)。得到自旋的概率分布,就可以推出一系列的宏观物理量。如net magnetization、能量、磁滞回线等。
因此问题的核心就在于如何解出自旋的概率分布?平均场近似假设:每个粒子所受到的外界作用(课堂上的例子是外界磁场作用)是周围所有粒子的平均。因此在公式(5)中,可以将\(q_i\)用\(<q>\)代替。经过这种方法处理,方程大为简化(不需要考虑周围粒子的反转等瞬态过程)由平均场近似可以得出一系列很好的结果:
- 相变温度Tc
- 相变磁场Hc
- 磁滞回线
- 区分一级相变二级相变
- \(<q> ~ (T_c-T)^{0.5}\)
平均场近似是不精确的。Onsager给出了二维Ising模型的解析接,序参量的critical exponent值不是0.5,而是0.125 。[1]
给同学们留下的作业是
1、回去动手算一下\(\tanh (Ax+b) = x\)的解。我用的是直接迭代。如果用牛顿迭代是不是收敛性更好?可否用程序证明?
2、算一下\(T^* = 0\) 和\(T^* > 0)时候的磁滞回线,看一下与低温时候有何区别?
资料:
[第二节课课件] [计算不同温度下的][计算磁滞回线的python程序]
python环境管理包:anaconda: https://www.anaconda.com/
python的IDE:spyder 可以在anaconda中下载
有用的包:
自行搜索手册、可用anaconda安装或者用pip安装
基本数学工具和数组:numpy
科学计算、求解方程: scipy (部分替代mathematica)
数据表: pandas (可替代excel)
绘图:matplotlib (可替代origin)
参考文献
[1] Onsager, Lars. “Crystal statistics. I. A two-dimensional model with an order-disorder transition.” Physical Review 65.3-4 (1944): 117.