相场模型(Phase field model)主要是为了解决界面问题。思想来源最早可以追溯到Van der Waals在处理液体表面张力时候的非均匀界面假设,经过Landau&Lifshitz、Allen-Cahn、Cahn-Hillard发展,日趋完善。对于相场模型的表达式,在简单、低维、平衡的条件下,人们已经给出了解析解。但是对于复杂的边界条件以及非平衡状态下序参量的演化过程,计算量十分庞大。
随着计算机科学的不断发展,求解复杂边界条件下的相场方程成为可能。典型的例子是R. Kayabushi(1993)的晶枝生长、以及LQ Chen等的铁电畴变的算例。目前相场方法应用于众多领域,如
- 铁电
- 铁磁
- 合金
- 马氏体相变
- 多相合金
- 粉末冶金
等等。
那么,究竟什么是相场模型?对于一个界面,我们可以有两种处理方式:
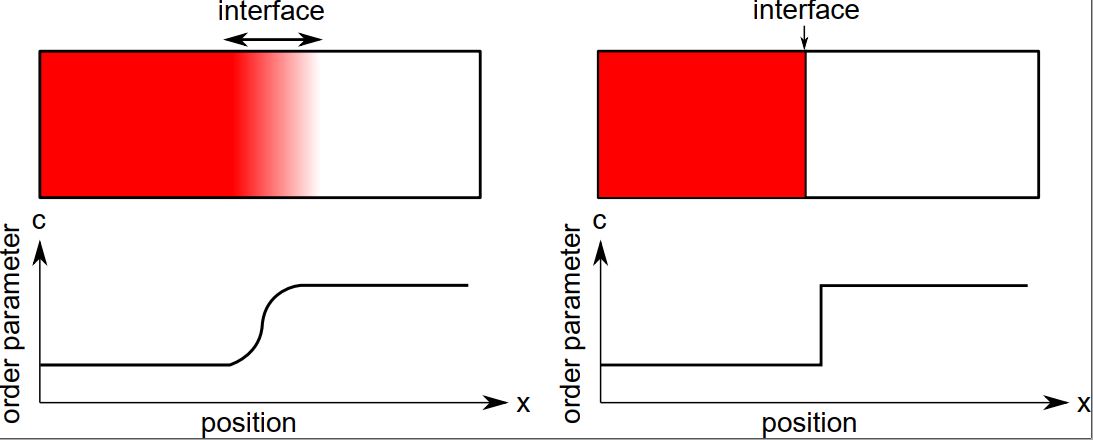
对于气、液界面,Tolman [1] 和Ono Kondo [2] 证明,采用如下所示的自由能表示方式,最后得到的界面的序参量是间断变化的。
\(\psi(z) = \psi(z) [\rho(z), T]\) (1)
自由能取最低的条件为表面张力为0。
Van der Waals 提出,在界面处的自由能分布不是均匀的,而是一个跟组份比例有关的参数:
\(\Psi(z) = \psi(z) [\rho(z), T]\) – \psi(\rho^{A,B}, T) (2)
与公式(1)相比增加的一部分自由能被称为surface excess。注意这里自由能的分布是位置坐标的函数。
Landau采用相同的思想,将铁磁体自由能的分布写为局部序参量(如magnetization)梯度的函数。Cahn等将梯度引入任意非均匀系统。在此假设下,自由能密度可以写为
\(\psi(c,\nabla c) = \psi _0(c) + G|\nabla c|^{2} \) (3)
其中c为系统的序参量,\( \psi _0(c) \) 为局部自由能密度, \( |\nabla c|^{2} \)为因序参量在空间分布的不均匀所导致的自由能的增加。 公式(3)即为平衡状态对应的相场公式。
与其他处理非均匀系统的方法相比, 相场法有着以下优点::
- 相场方法对于界面的追踪是自动的。通过将体系自由能朝着能量最小的方向演化,可以自动获得界面的变化。
- 相场方法是处理非平衡状态过程有力工具。
- 相场的相参数可以与其它外场,如温度场、电场等进行耦合。
参考文献
[1] Tolman, Richard C. “The effect of droplet size on surface tension.” The journal of chemical physics 17.3 (1949): 333-337.
[2] Ono, Syu, and Sohei Kondo. “Molecular theory of surface tension in liquids.” Structure of Liquids/Struktur der Flüssigkeiten. Springer, Berlin, Heidelberg, 1960. 134-280.
[3] Cahn, John W., and John E. Hilliard. “Free energy of a nonuniform system. I. Interfacial free energy.” The Journal of chemical physics 28.2 (1958): 258-267.